Production domestique

Une version étendue du modèle néoclassique travail-loisir

Ce chapitre s’appuie sur le chapitre 6 du livre de Blau et Winkler (voir syllabus).

Jusqu’à présent, nous avons supposé que les individus allouent leur temps entre le travail rémunéré et le loisir. Cependant, dans la pratique, une grande partie de notre temps est également consacrée à des activités domestiques, telles que cuisiner, faire la lessive et s’occuper des enfants ou des parents âgés.
En France, les personnes passent en moyenne trois heures par jour sur les tâches domestiques (voir la dernière enquête sur l’utilisation du temps de l’INSEE). Notamment, les femmes consacrent beaucoup plus de temps à ces activités que les hommes, surtout si elles ont des enfants. Alors que les mères ayant des enfants à charge consacrent environ cinq heures par jour aux tâches domestiques, leurs partenaires masculins n’y consacrent qu’environ la moitié de ce temps.

Définition

Désormais, nous utiliserons le mot “travail” pour désigner le temps consacré au travail rémunéré. C’est-à-dire que, comme auparavant, nous nous référerons au travail marchand et non au travail domestique.

Dans ce chapitre, nous allons introduire le temps domestique dans le modèle néoclassique travail-loisir que nous avons vu précédemment.
Notre objectif sera de comprendre comment les femmes avec enfants à charge allouent leur temps entre la maison et le travail. Nous allons explorer comment elles décident de travailler, et si oui, pour combien d’heures. Avec ce modèle étendu à l’esprit, nous examinerons ensuite comment les mères peuvent changer leurs décisions d’offre de travail en recevant des subventions à la garde d’enfants.

Avant d’entrer dans notre modèle théorique, notez que nous ne traiterons pas de la manière dont les couples prennent des décisions conjointes sur leur allocation de temps.
Au lieu de cela, pour simplifier, nous allons nous concentrer sur un unique décideur, généralement une mère avec des enfants à charge, qu’elle soit célibataire ou mariée.
Cependant, nous tiendrons compte de son contexte familial en incluant les revenus des autres membres de la famille dans son revenu non salarié.
Les changements dans les revenus de ses proches (en particulier, de son partenaire) modifieront à leur tour la contrainte budgétaire de la mère et son choix optimal.

Préférences

Nous supposons que l’individu tire satisfaction (utilité) de la consommation des biens et services produits avec des biens/services marchands et du temps non marchand (temps domestique).
Les biens et services qu’elle aime consommer peuvent inclure un dîner avec des amis à la maison, des enfants en bonne santé, une maison propre ou de courtes vacances. Tous ceux-ci nécessitent non seulement d’acheter des biens et services sur le marché (tels que des ingrédients alimentaires, des produits de nettoyage, et des billets de transport), mais aussi d’y consacrer son propre temps (en cuisinant, en jouant avec les enfants, en faisant le ménage, en organisant un voyage, etc.).

Comme dans les chapitres précédents, nous supposons que l’individu choisit le panier de biens marchands et temps non marchand qui maximise son utilité, compte tenu de sa contrainte budgétaire. Bien que ces facteurs de production ne lui apportent pas directement d’utilité, ils contribuent à produire les biens et services qu’elle aime. Nous pouvons donc exprimer la fonction d’utilité de l’individu en termes de biens marchand $(C_{M})$ et de temps non marchand $(h_{NM})$, les deux facteurs permettant produire ce qu’elle aime consommer.
Les courbes d’indifférence représentant cette fonction d’utilité indirecte remplissent les mêmes propriétés discutées dans les chapitres précédents.
La figure ci-dessous montre deux courbes d’indifférence.

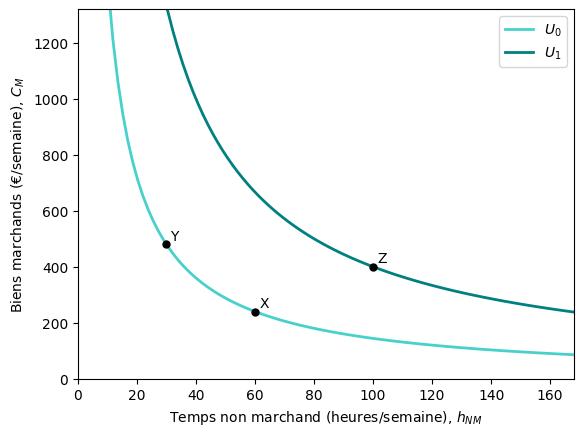
Pour rappel, chaque courbe d’indifférence montre les différentes combinaisons de biens marchands $(C_{M})$ et de temps non marchand $(h_{NM})$ donnant le même niveau d’utilité.
De plus, la pente de ces courbes capture combien l’individu est prêt à substituer des biens marchands au temps non marchand. Cette pente est plus raide lorsque le temps non marchand est relativement rare : lorsque l’individu dispose de beaucoup de biens marchands mais de peu de temps non marchand, elle est moins prête à renoncer à ce temps pour obtenir davantage de biens achetés.

Substitution entre biens marchands et temps non marchand

Contrairement aux chapitres précédents, l’individu peut maintenant substituer des biens marchands au temps non marchand de deux manières, dans la consommation et la production.
Discutons chacune d’elles.

Substitution dans la consommation

De manière générale, certaines biens et services nécessitent de grandes quantités de biens/services marchands mais peu de temps non-marchand, tandis que d’autres nécessitent l’inverse. Par exemple, comparez un dîner entre amis dans un restaurant étoilé à un dîner avec eux à la maison. Le premier peut coûter une bonne part de votre salaire journalier mais peu de temps personnel, tandis que le second peut être nettement plus abordable mais nécessiter beaucoup de temps pour cuisiner et nettoyer après le départ des invités.

La substitution dans la consommation implique donc de substituer des biens/services qui sont intensifs en biens marchands à ceux intensifs en temps non marchand (ou vice versa). Par exemple, l’individu peut être prêt à substituer un dîner dans un restaurant étoilé par deux dîners organisés chez elle.

Substitution dans la production

Dans de nombreux cas, le même bien/service peut être produit avec soit de grandes quantités de biens/services marchands soit beaucoup de temps non marchand. Par exemple, vous pouvez avoir une maison propre soit en embauchant quelqu’un, soit en la nettoyant vous-même.

La substitution dans la production consiste donc à substituer des techniques de production qui sont intensives en biens marchands à celles intensives en temps non marchand (ou l’inverse).

Comparaison des courbes d’indifférence entre individus

La pente d’une courbe d’indifférence reflète l’ampleur de la substitution entre les biens marchands et le temps non-marchand, tant au niveau de la consommation que de la production.

En particulier, les individus qui attachent une valeur relative plus élevée aux biens de consommation intensifs en temps auront des courbes d’indifférence plus raides. Par exemple, certaines personnes peuvent simplement valoriser hautement le fait d’accueillir des amis pour un dîner. Ces individus ne seront donc pas facilement convaincus de substituer des biens marchands au temps non-marchand, du moins en ce qui concerne le dîner entre amis.

De plus, ceux qui supportent une plus grande charge de travail domestique et de responsabilités familiales trouveront plus difficile de renoncer à du temps non-marchand dans la production, ayant ainsi aussi des courbes d’indifférence plus raides. En particulier, les femmes avec des familles qui adhèrent à des rôles de genre traditionnels peuvent ressentir une pression sociale pour passer plus de temps à la maison. Si tel est le cas, elles auront plus de mal à substituer des biens marchands à leur temps domestique pour “produire” des enfants en bonne santé, des repas nutritifs, une maison propre, etc.

La contrainte budgétaire

Nous supposons que l’individu a $T$ heures par semaine à allouer entre les activités de marché et les activités non-marchandes (domestiques).
De plus, elle a $V$ euros par semaine de revenu non salarial (qui peut inclure le revenu d’un partenaire), et reçoit un salaire de $w$ euros pour chaque heure travaillée sur le marché du travail.

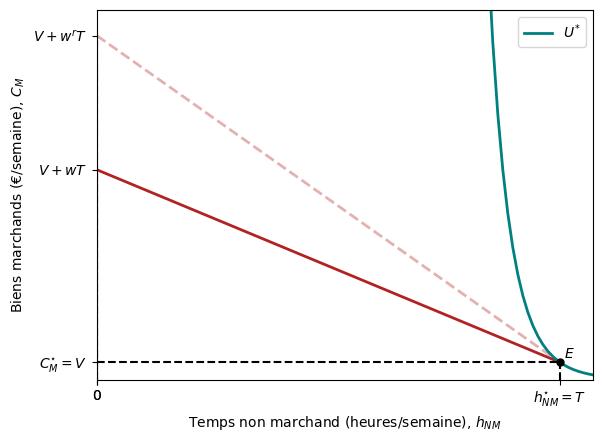
La figure ci-dessous montre la contrainte budgétaire de l’individu : toutes les combinaisons de temps non-marchand et de biens de marchands parmi lesquelles elle peut choisir, compte tenu de son revenu non salarial et de son salaire.

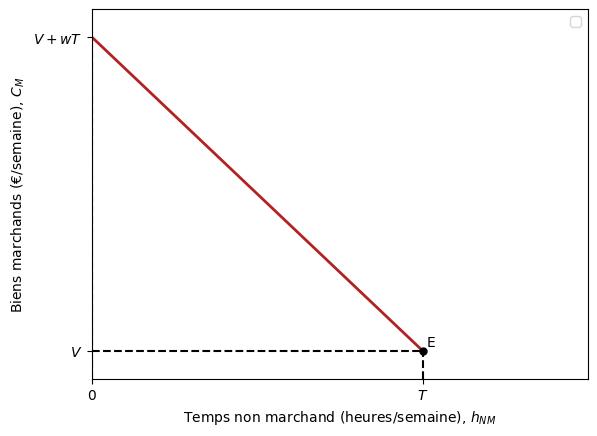
Comme nous l’avons fait précédemment, nous appellerons le panier $E$ dans la figure le “point de dotation”.

La décision de travailler

Comme dans le modèle simple travail-loisir que nous avons vu précédemment, l’individu choisira de travailler si son salaire de marché $(w)$ est supérieur à son salaire de réserve $(w^{r})$.

Rappel

Le salaire de réserve $(w^{r})$ est la compensation monétaire qui rend l’individu indifférent entre travailler ou ne pas travailler sur le marché du travail.

Étant donné la contrainte budgétaire dans la figure précédente, le salaire de réserve de l’individu est égal à la pente de la courbe d’indifférence (en valeur absolue) au point de dotation $E$.

Par conséquent, l’individu choisira de rejoindre la force de travail si et seulement si :

$$w>w^{r}=\left(\frac{MU_{h_{NM}}}{MU_{C_{NM}}}\right)_{\bigr\rvert h_{NM}=T,C_{NM}=V}$$

Ainsi, nous pouvons prédire que, toutes choses égales par ailleurs, les femmes seront plus susceptibles de travailler si elles ont des salaires plus élevés (si leur temps de marché est mieux rémunéré). En revanche, elles seront moins susceptibles de travailler si leurs courbes d’indifférence sont plus raides (si elles attribuent plus de valeur au temps non-marchand).

La valeur du temps marchand $\boldsymbol{(w)}$

Des salaires plus élevés augmentent le coût d’opportunité du temps passé dans des activités non-marchandes. Ainsi, ils augmentent la propension des femmes à travailler par un effet de substitution. Cela ne signifie pas qu’une augmentation de salaire donnée va tirer toutes les femmes inactives dans la force de travail. Certaines auront des salaires de réserve trop élevés pour les inciter à travailler. Cependant, d’autres avec des salaires de réserve plus faibles commenceront à travailler. La figure ci-dessous illustre ce second cas.

À un salaire initial de $w_{0}$, l’individu maximise son utilité en restant à son point de dotation $E$, c’est-à-dire qu’elle reste en dehors de la force de travail $(w_{0}<w^{r})$.
Cependant, à un nouveau salaire de $w_{1}>w_{0}$, elle maximise son utilité en passant au panier $B$, choisissant d’entrer sur le marché du travail $(w_{1}>w^{r})$.

Cet effet prédit des salaires sur la participation au marché du travail peut partiellement expliquer pourquoi les femmes (et les hommes) ayant des niveaux d’éducation plus élevés sont plus susceptibles de travailler.
Par exemple, en France, les femmes diplômées du supérieur sont 18 points de pourcentage plus susceptibles de participer au marché du travail que celles qui n’en ont pas (voir “Quelle influence du diplôme sur la participation au marché du travail ?” par France Stratégie).
Notez, cependant, que cette corrélation entre l’éducation et la participation au marché du travail peut non seulement refléter l’effet causal des salaires sur les incitations à travailler, mais aussi une “auto-sélection” : ces femmes qui prévoient de travailler davantage au cours de leurs années d’adulte (car, par exemple, elles ou leurs familles valorisent davantage le “succès” professionnel) peuvent choisir d’investir plus dans leur éducation.

La valeur du temps non marchand $\boldsymbol{(w^{r})}$

Préférences

La valeur du temps non marchand dépend des goûts de l’individu et des restrictions pour substituer des biens marchands au temps non-marchand. En particulier, les femmes avec un goût plus prononcé pour le temps non marchand, ou avec des contraintes plus strictes pour le substituer avec des biens marchands, auront des courbes d’indifférence plus raides, donc des salaires de réserve plus élevés. Ainsi, toutes choses égales par ailleurs, ces femmes seront moins susceptibles de rejoindre la population active.

Les goûts et les restrictions pour substituer des biens marchands au temps hors du marché du travail peuvent dépendre fortement de la présence de nourrissons et de jeunes enfants.
Considérons deux femmes différentes : Camille qui a un enfant à charge de plus de cinq ans et Marine qui a un petit enfant de moins de douze mois. Tous les autres facteurs étant égaux, nous pouvons nous attendre à ce que Marine soit moins susceptible que Camille de choisir de travailler. En effet, bien que les femmes puissent acheter des services de garde d’enfants sur le marché, elles peuvent avoir besoin et vouloir s’occuper de leurs enfants elles-mêmes, surtout lorsqu’elles ont des petits enfants. Si tel est le cas, les courbes d’indifférence de Marine seront plus raides que celles de Camille. Cette pente plus raide reflète que Marine, qui a un enfant de moins de 12 mois, a plus de mal à utiliser des techniques de production qui sont intensives en biens marchands (substitution dans la production), comme manger au restaurant. En outre, cela reflète qu’elle a une préférence plus prononcée pour consommer des biens qui demandent plus de temps domestique (substitution dans la consommation), comme s’occuper de son enfant elle-même.

Les deux figures ci-dessous illustrent le choix optimal de Camille et Marine. Nous supposons qu’elles ont le même salaire de marché $w$ et revenu non salarial $V$. De plus, nous supposons qu’elles ont des préférences identiques pour les biens marchands et le temps non marchand, à l’exception de leurs responsabilités familiales et de leurs préférences en tant que mères.

Camille rejoint la force de travail : $w > w^{r}$  

 

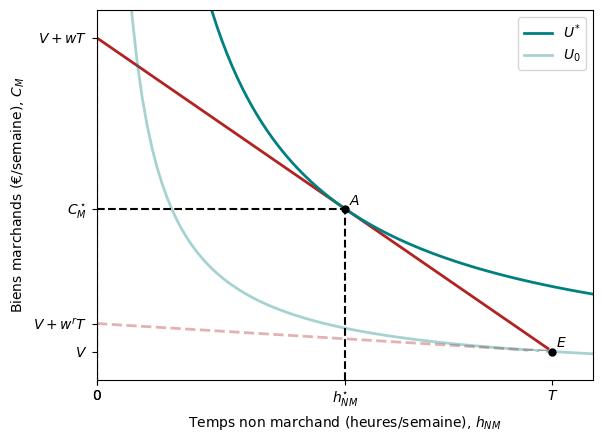
Marine ne rejoint pas la force de travail : $w \leq w^{r}$  

Il est important de noter que les goûts et les restrictions des femmes concernant l’échange de temps domestique contre des biens marchands peuvent également être influencés par des normes sociales et des attitudes envers leur rôle sur le marché du travail et au sein du ménage. Toutes choses égales par ailleurs, les femmes seront moins susceptibles de travailler, ou travailleront moins d’heures, si leurs familles adhèrent à la division traditionnelle du travail dans laquelle les hommes se spécialisent dans le travail de marché et les femmes dans le travail domestique.

Revenu non salarial

La valeur du temps non marchand dépend également du revenu non salarial de l’individu, qui peut inclure les revenus d’un partenaire. Pour les personnes mariées, la source principale de revenu non-salarié est souvent le revenu de leur conjoint.

Hypothèse

Nous supposons que le temps non marchand est un bien “normal”. C’est-à-dire que nous supposons que l’individu demande plus de temps non marchand (d’où elle travaille moins) lorsque son revenu augmente (à salaire constant). Dans le modèle travail-loisir que nous avons abordé dans les chapitres précédents, nous avons aussi supposé que le loisir (également le temps passé en dehors du marché du travail) était un bien normal.

Ainsi, un revenu non salarial plus élevé augmente la demande de temps non marchand, et réduit les heures de travail sur le marché, par un effet revenu.

En fait, certains individus peuvent se retirer complètement du marché du travail lorsque leur revenu non salarial est élevé. Donc, toutes choses égales par ailleurs, les femmes dont les partenaires gagnent plus sont moins susceptibles de travailler. La figure ci-dessous illustre cet effet.

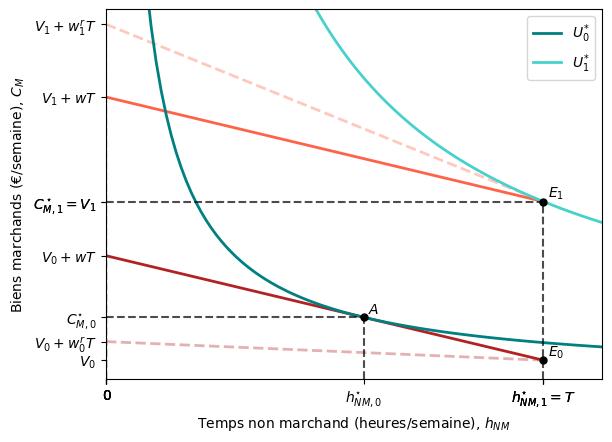
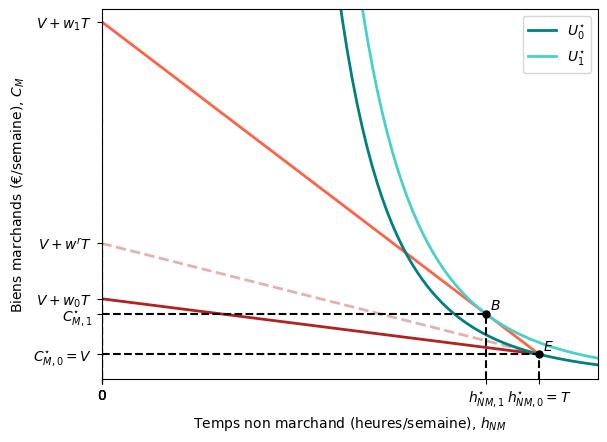
Lorsque son revenu non salarial s’élève à $V_{0}$, l’individu maximise son utilité en choisissant le panier $A$, travaillant donc $T-h_{NM,0}^{\star}$ heures par semaine (et consommant $C_{M,0}^{\star}$ euros/semaine de biens marchands).
Néanmoins, une fois que son revenu non salarial atteint $V_{1}$, elle maximise son utilité en étant à son nouveau point de dotation $(E_{1})$, quittant ainsi le marché du travail.

Pourquoi son nouveau revenu non salarial l’incite-t-il à faire ce choix ?
Un revenu non salarial plus élevé $(V_{1}>V_{0})$ augmente le salaire de réserve de l’individu $(w_{1}^{r}>w_{0}^{r})$ en lui permettant de consommer plus de biens marchands à son point de dotation, augmentant ainsi la valeur relative du temps non marchand à 0 heures de travail.
En d’autres termes, l’individu a besoin d’une compensation plus élevée pour renoncer à une heure de temps non marchand si elle peut consommer “beaucoup de” biens marchands sans faire de travail rémunéré.
Dans la figure ci-dessus, l’augmentation du revenu non salarial de l’individu est suffisamment importante pour porter son salaire de réserve au-dessus de son salaire de marché $(w_{1}^{r}>w)$, ce qui l’incite à quitter complètement le marché du travail.

La figure illustre également que les femmes mariées, qui ne sont pas dans la force de travail, seront plus susceptibles de travailler si le revenu de leurs maris diminue (par exemple, s’ils perdent leur emploi lors d’une récession économique).
Cet effet est appelé le “effet du travailleur ajouté”.

Heures de travail

Ceux qui rejoignent la force de travail maximisent leur utilité en travaillant jusqu’à ce que leur taux marginal de substitution entre les biens marchands et le temps non marchand (en valeur absolue) soit égal à leur salaire de marché.

C’est-à-dire, $$\left(\frac{MU_{h_{NM}}}{MU_{C_{M}}}\right)_{\bigr\rvert h_{NM}^{\star},C_{NM}^{\star}}=w$$

Les heures de travail optimales des femmes $(T-h_{NM}^{\star})$ dépendent donc de leurs goûts et leurs contraintes pour substituer du temps non marchand par des biens du marché (côté droit de la condition ci-dessus). Par exemple, les femmes qui sont plus orientées vers la carrière trouveront optimal de travailler plus d’heures, tous les autres facteurs étant égaux. En outre, les femmes ayant des petits enfants choisiront de travailler moins.

Le choix des heures de travail des femmes dépend également de leur revenu non salarial. En effet, comme nous l’avons mentionné auparavant, un revenu non salarial plus élevé augmente la demande de temps non-marchand et réduit ainsi les heures de travail sur le marché (effet revenu).

Enfin, les heures de travail des femmes dépendent également du salaire de marché qu’elles peuvent obtenir. Des salaires plus élevés leur permettent de consommer plus de biens marchands et de temps non-marchand, les incitant ainsi à travailler moins d’heures (effet revenu). Néanmoins, des salaires plus élevés augmentent aussi le coût d’opportunité du temps non-marchand, encourageant ainsi les femmes à travailler plus d’heures (effet de substitution). L’effet net de ces deux forces est théoriquement ambigu. Cependant, la plupart des études empiriques suggèrent que l’effet de substitution domine.

Exercices

Les exercices suivants sont extraits du Chapitre 6 du livre d’Ehrenberg et al. (voir le syllabus).

Exercice 1

La phrase suivante est-elle vraie, fausse ou incertaine ? Pourquoi ?

“Si le conjoint d’une femme obtient une augmentation de salaire, elle a tendance à travailler moins, mais si c’est elle qui obtient une augmentation, elle a tendance à travailler plus.”

Exercice 2

Le gouvernement souhaite fournir des incitations pour que les mères célibataires entrent sur le marché du travail et obtiennent un emploi. En particulier, le gouvernement envisage de payer 20 euros par jour aux mères célibataires ayant de jeunes enfants si elles travaillent au moins six heures par jour, cinq jours par semaine.

Tracez une contrainte budgétaire journalière actuelle pour une mère célibataire, puis tracez la contrainte qui serait créée par la subvention de 20 euros. Discutez des effets probables sur la participation au marché du travail et les heures travaillées des mères éligibles à la subvention.