L’offre de travail

Une étude plus approfondie de l’offre de travail : Une théorie de la décision de travailler

Plus tôt ou plus tard, nous sommes tous confrontés à deux décisions importantes : travailler ou non et, si nous rejoignons le marché du travail, combien d’heures travailler. Dans ce chapitre, nous allons étudier le cadre de base que les économistes utilisent pour analyser ces décisions, le modèle néoclassique du choix travail-loisir. Dans ce cadre, les personnes (travailleurs) choisissent comment dépenser leurs ressources limitées (temps et richesse) entre les choses qu’elles aiment. Elles aiment consommer des biens (de pain et de lait à des vêtements de luxe) et du temps de loisir (pensez, par exemple, à regarder un film ou passer du temps avec des amis). Les biens doivent être achetés sur le marché, ils nécessitent donc de dépenser de l’argent. Les gens doivent donc travailler pour gagner de l’argent et acheter les biens qu’ils aiment. Nous supposons que les travailleurs choisissent la combinaison de biens et de loisirs qui maximise leur utilité (ou leur bien-être). Puisque le temps est limité, ils sont confrontés à un arbitrage économique entre la consommation de biens et les loisirs : s’ils travaillent beaucoup, ils peuvent acheter de nombreux biens qui les rendent heureux, mais il leur restera peu de temps libre à consacrer à leurs loisirs. Au contraire, s’ils travaillent peu, ils disposent de beaucoup de temps libre mais ne peuvent se permettre que peu des biens qu’ils aiment.

Les préférences du travailleur

Pensons à un travailleur individuel. Comme nous l’avons dit, nous supposons qu’une personne tire satisfaction de la consommation de biens et de temps de loisir. Bien entendu, cette personne peut consommer différents biens. Mais, pour simplifier, nous additionnons la valeur monétaire de tous les biens qu’il ou elle consomme au cours d’une période donnée et nous la désignons par $C$ (qui, nous le dirons, est mesuré en euros). Par exemple, $C=1000$ euros peut inclure l’argent dépensé pour la nourriture, le loyer, les tickets de bus, les nouveaux vêtements, etc. $L$ désigne le nombre d’heures de loisir que la personne profite sur la même période de temps.

Utilité et courbes d’indifférence

L’idée que le bien-être ou le bonheur du travailleur dépend à la fois de la consommation de biens et de loisir est capturée par la fonction d’utilité :

$U=f(C,L)$.

Vous pouvez penser à cette fonction d’utilité comme une “machine” transformant les ressources dépensées en biens et loisir (entrées) en un indice $U$ qui mesure le niveau de bien-être que le travailleur obtient en les consommant (sortie). Nous supposons que plus le travailleur consomme de biens ou de loisir, plus il est heureux, c’est-à-dire plus son utilité est élevée.

Tout comme il existe de nombreuses façons de passer un joyeux week-end, l’intuition nous dit qu’il peut y avoir différentes combinaisons de biens de consommation (mesurés par $C$) et de loisirs (mesurés par $L$) qui pourraient laisser notre travailleur également heureux (obtenant le même niveau d’utilité).

Supposons que notre travailleur consomme 480 euros de biens et 30 heures de loisir par semaine (point $Y$ dans la figure ci-dessous).

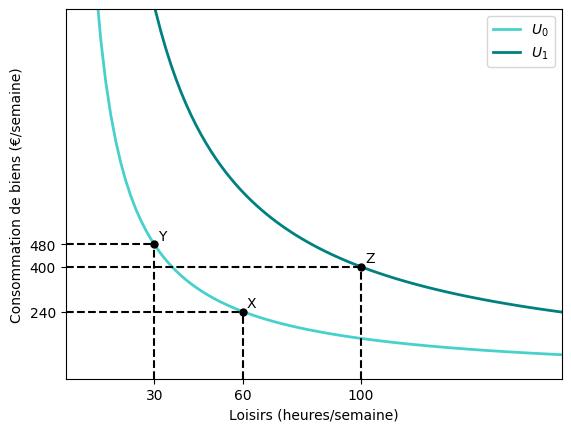
Et, disons que ce panier de consommation lui donne 120 utils (l’unité de mesure de son utilité). Maintenant, supposons que notre travailleur pourrait obtenir le même niveau d’utilité en consommant 480 euros de biens et 60 heures de loisir (point $X$ dans la figure). Si nous joignions tous les points qui donnent à notre travailleur le même niveau d’utilité (120 utils), nous obtiendrions une courbe d’indifférence comme celle étiquetée $U_{0}$ dans la figure.

Supposons maintenant que le travailleur consomme plus de biens et plus de loisir. Cette nouvelle combinaison de biens et de loisir le rendrait certainement plus heureux, après tout, (par hypothèse) il aime les deux. Une combinaison comme celle-ci est représentée par le point $Z$ dans la figure ci-dessus. Puisque $Z$ a plus de biens et plus de loisir, il se trouve sur une courbe d’indifférence plus élevée, étiquetée $U_{1}$ et représentant 200 utils. Comme vous pouvez le constater, nous pouvons donc parler d’une “famille” de courbes d’indifférence, chacune représentant un niveau d’utilité différent pour le travailleur.

Les courbes d’indifférence remplissent quatre propriétés importantes :

Les courbes d’indifférence plus hautes représentent des niveaux d’utilité plus élevés puisque, par hypothèse, les travailleurs sont plus heureux s’ils peuvent consommer davantage de toutes les choses qu’ils aiment (biens et loisirs).
Les courbes d’indifférence ne se croisent pas. Pourquoi? Cette propriété découle de la définition d’une courbe d’indifférence et de l’hypothèse selon laquelle plus de biens et de loisir rendent le travailleur plus heureux. Pensez à trois différents paniers de biens et de loisir. Imaginez que les deux premiers rendent le travailleur également heureux, ils appartiennent donc à la même courbe d’indifférence. C’est le cas des paniers $X$ et $Y$ dans la figure ci-dessous.

Prenez maintenant un troisième panier ayant plus de biens et de loisir que $X$, comme $Z$ dans la figure. $Z$ rend le travailleur plus heureux que $X$ puisqu’il a plus de biens et plus de loisir : il rapporte $U_{1}>U_{0}$ utils. Mais la courbe d’indifférence représentant $U_{1}$ peut-elle croiser celle de $U_{0}$ ? Non. Si c’était le cas, comme le montre la figure ci-dessus, cela conduirait à une contradiction. En effet, cela signifierait que le travailleur est indifférent entre $X$ et $Y$ et entre $Y$ et $Z$ mais, si tel est le cas, il devrait l’être entre $X$ et $Z$. Cependant, prétendre que le travailleur est indifférent entre $X$ et $Z$ contredirait notre hypothèse selon laquelle plus de biens et de loisir rendent le travailleur plus heureux.
Les courbes d’indifférence ont une pente négative. Encore une fois, cette propriété découle de la définition des courbes d’indifférence et de l’hypothèse selon laquelle les travailleurs aiment consommer à la fois des biens et du loisir. Jetez un autre coup d’œil aux paniers $Y$ et $X$ dans la première figure ci-dessus. Avec le panier $Y$, le travailleur consomme 480 euros de biens et 30 heures de loisir par semaine, ce qui lui donne $U_{0}$ utils. Si le travailleur consommait plus de loisirs (disons 60 heures), pourrait-il également consommer plus de biens et être aussi heureux qu’avant (aussi heureux que $U_{0}$ utils) ? Non, car, par hypothèse, s’il consomme plus de biens et de loisirs, il sera plus heureux. Par conséquent, tous les paniers situés sur une courbe d’indifférence donnée échangent des biens de consommation contre des loisirs. Si nous profitons d’une heure de loisir supplémentaire, nous devons renoncer à certains biens de consommation si nous voulons maintenir constant notre niveau d’utilité. Nous pourrions également dire que si nous devons vivre avec moins de biens que nous aimons, nous devrons profiter de plus de loisirs pour compenser les biens que nous n’achetons plus, c’est-à-dire pour maintenir notre utilité constante.
Les courbes d’indifférence sont convexes (plus raides à gauche qu’à droite). Nous venons de dire que la seule façon de consommer plus de loisirs, tout en ayant la même utilité, est de renoncer à certains des biens que nous aimons. Mais, bien sûr, l’intuition nous dit que plus nous avons de loisirs, moins nous en profitons. Et, par conséquent, moins nous serons disposés à renoncer à des biens en échange de loisirs. Cette volonté d’échanger des biens contre des loisirs est représentée par la pente d’une courbe d’indifférence. Par conséquent, dire que les courbes d’indifférence sont convexes revient à faire l’hypothèse supplémentaire que la volonté des travailleurs d’échanger des biens contre des loisirs diminue à mesure que les loisirs deviennent relativement abondants.

Voyons maintenant pourquoi la pente d’une courbe d’indifférence indique le nombre d’euros de biens que le travailleur est prêt à abandonner pour une heure de loisir supplémentaire (ou encore, le nombre d’euros de biens supplémentaires dont il a besoin pour renoncer à une heure de loisir).

La pente d’une courbe d’indifférence

Quel serait le degré de satisfaction du travailleur s’il consommait une heure supplémentaire de loisir ou un euro supplémentaire de biens ? L’utilité marginale du loisir (notée $MU_{L}$) mesure la variation de l’utilité du travailleur lorsqu’il consomme une heure supplémentaire de loisir, en gardant constant ce qu’il dépense en biens. De même, l’utilité marginale de la consommation (notée $MU_{C}$) mesure la variation de son utilité lorsqu’il dépense un euro supplémentaire en biens de consommation, à temps de loisir constant. Puisque nous avons supposé que le loisir et les biens rendent le travailleur heureux, leurs utilités marginales doivent être positives : une unité supplémentaire de l’un d’eux, en maintenant l’autre constante, augmente l’utilité du travailleur.

Nous avons vu précédemment que des courbes d’indifférence plus élevées représentent des niveaux d’utilité plus élevés. En d’autres termes, les mouvements des courbes d’indifférence vers le nord-est rendent le travailleur plus heureux. Mais qu’en est-il des mouvements le long des courbes d’indifférence ? Par construction, le travailleur est indifférent entre toute combinaison de loisirs et de biens située sur une courbe d’indifférence donnée. Considérons les paniers $X$ et $Y$ de la figure ci-dessous (la même que celle que nous avons vue au début de ce chapitre).

Le travailleur est indifférent entre consommer :

60 heures de loisir et 240 euros de biens ($X$) et
30 heures de loisir et 480 euros de biens ($Y$).

Par conséquent, un mouvement de $X$ vers $Y$ implique que le travailleur a besoin de 240 euros supplémentaires de biens pour renoncer à 30 heures de loisir et maintenir son utilité constante. Si nous permettions à $Y$ d’être “très proche “ de $X$ et que nous calculions la variation de la valeur en euros des biens par variation des heures de loisir, nous trouverions la pente de la courbe d’indifférence. Cette pente mesure combien d’euros supplémentaires de biens convaincraient le travailleur de renoncer à une “petite “ quantité de loisir. Ce taux de variation est appelé le taux marginal de substitution des biens de consommation aux loisirs (en anglais, marginal rate of substitution of consumption goods for leisure, MRS). Il s’avère qu’il est égal à la valeur négative de l’utilité marginale relative des loisirs par rapport à celle de la consommation. C’est-à-dire, $$MRS_{C \text{ for } L} \equiv \frac{dC}{dL} = -\frac{MU_{L}}{MU_{C}}$$

Pour démontrer la dernière égalité, utilisez l’équation suivante : $$ dU = MU_{C}dC + MU_{L}dL $$ où $dC$ et $dL$ désignent des “petits” changements de $C$ et $L$, et $dU$ la variation totale de l’utilité provenant de ces dernières.

Par définition, une courbe d’indifférence montre toutes les combinaisons de biens et de loisirs produisant le même niveau d’utilité. Par conséquent, le long de toute courbe d’indifférence, $$dU=0.$$ D’où, $$0 = MU_{C}dC + MU_{L}dL.$$ $$\frac{dC}{dL} = -\frac{MU_{L}}{MU_{C}}$$

L’hypothèse selon laquelle les courbes d’indifférence sont convexes (plus raides à gauche qu’à droite) implique que le taux marginal de substitution diminue à mesure que le travailleur a plus de loisirs et moins de consommation. En d’autres termes, le travailleur est moins disposé à échanger des biens de consommation contre des loisirs à mesure que son temps de loisir devient relativement abondant.

Différences de préférences entre les travailleurs

Les courbes d’indifférence peuvent varier considérablement d’un travailleur à l’autre. Certaines personnes font de leur travail une véritable passion ou, du moins, une expérience agréable. D’autres considèrent le travail comme une simple source de revenus et accordent beaucoup plus d’importance aux loisirs.

Ces préférences différentes se traduisent par des taux marginaux de substitution différents entre les biens de consommation et les loisirs. Les figures suivantes illustrent les préférences de deux travailleurs, Pascale et Florent.

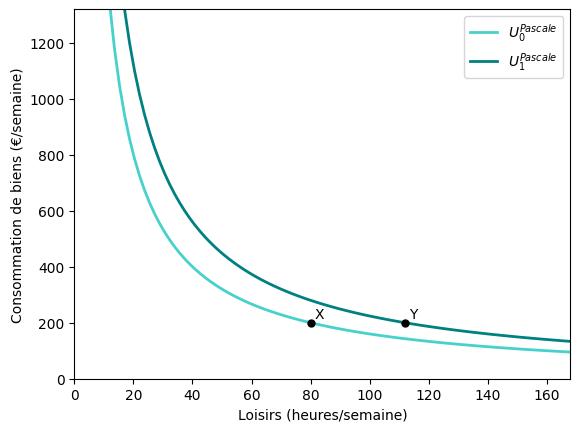
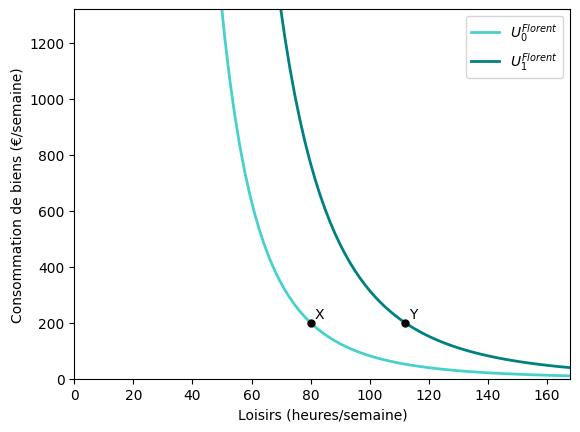
Les courbes d’indifférence de Florent sont plus raides : il n’est prêt à renoncer à une heure de loisir que s’il obtient une compensation monétaire importante en biens. En revanche, les courbes d’indifférence de Pascale sont plus plates : Elle est prête à renoncer à une heure de loisir pour une petite compensation monétaire.

La contrainte budgétaire

Les gens font des choix parce qu’ils ont des ressources limitées. Ici, le travailleur a deux contraintes : un montant donné de revenu à dépenser et 24 heures par jour.

Soit $V$ le “revenu *non salarial” du travailleur (la partie de son revenu qui est indépendante du nombre d’heures qu’il travaille) et $h$ le nombre d’heures qu’il travaille (par exemple, dans une semaine). La contrainte budgétaire du travailleur est alors la suivante : $$C=wh+V$$

En d’autres termes, la somme d’argent qu’il consomme en biens ($C$), au cours d’une période donnée, doit être égale à son revenu du travail ($wh$) plus son revenu non salarial ($V$).

Ici, nous faisons implicitement deux hypothèses pour pour rester simples : 1) le travailleur consomme tout son revenu et n’épargne donc pas, et 2) il reçoit le même salaire horaire quel que soit le nombre d’heures qu’il a travaillées.

Représentons maintenant la contrainte budgétaire du travailleur en termes de deux choses qu’il aime : les biens de consommation ($C$) et les loisirs ($L$). Le travailleur consacre la totalité de son temps disponible ($T$) au travail ou aux loisirs. C’est-à-dire, $$T=h+L$$

Par conséquent, $$C=w(T-L)+V$$

$$C=(wT+V)-wL$$

Cette ligne budgétaire montre combien le travailleur peut dépenser en biens de consommation ($C$) pour tout choix de loisir ($L) qu’il fait.

Cette ligne est représentée dans la figure suivante.

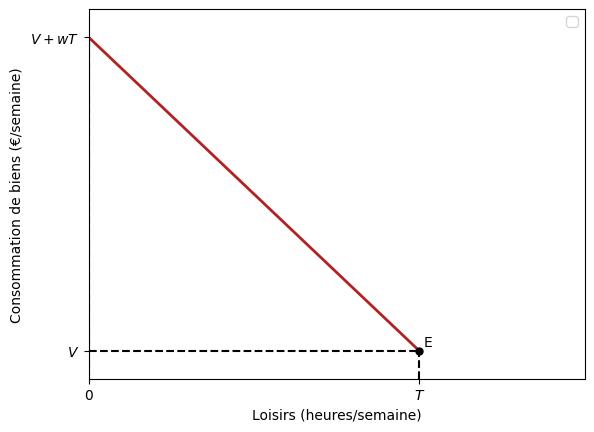
Comme le montre la figure, même si le travailleur décidait de ne pas travailler du tout, il serait toujours en mesure de consommer pour $V$ euros de biens (son revenu non salarial). Le point $E$ représentant cet panier de loisirs et de biens de consommation est appelé point de dotation. Chaque heure de travail supplémentaire (c’est-à-dire chaque heure de loisir abandonnée) permet au travailleur de consommer $w$ euros de biens de plus.

Tous les paniers situés sur ou sous la ligne de budget sont des paniers que le travailleur peut s’offrir ; ils constituent l’ensemble des opportunités (les “opportunités” que le travailleur peut saisir).

Nous allons maintenant parler du choix optimal du travailleur. Nous commençons par supposer que le travailleur trouve optimal de travailler et doit choisir le nombre d’heures de travail. Nous nous concentrerons ensuite sur la décision de travailler ou non.

Combien d’heures travailler ?

Comme nous l’avons dit au début, nous supposons que le travailleur choisit le panier de biens de consommation et de loisirs qui maximise son utilité. En d’autres termes, il choisit le panier qui lui permet d’atteindre le niveau d’utilité le plus élevé (courbe d’indifférence la plus haute) compte tenu de sa contrainte budgétaire.

La figure ci-dessous illustre cette offre optimale, étiquetée $A$ dans la figure.

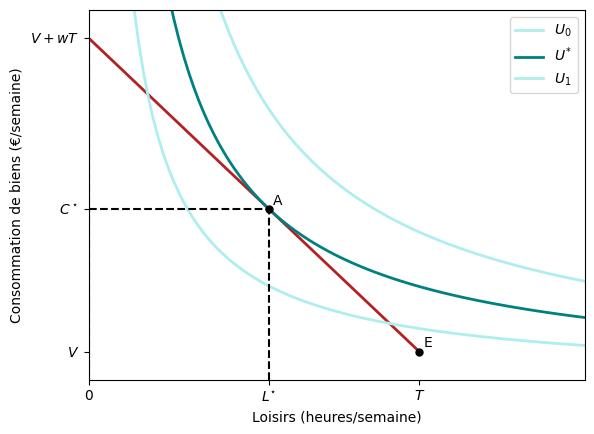
Comme nous pouvons le voir, cet panier optimal est celui où la pente de la courbe d’indifférence est égale à la pente de la contrainte budgétaire (où la courbe d’indifférence est tangente à la contrainte budgétaire). C’est-à-dire, $$MRS_{C \text{ for } L} = -w$$ $$-\frac{MU_{L}}{MU_{C}}=w$$ $$\frac{MU_{L}}{MU_{C}}=w$$

Cette condition de tangence nous indique que, au panier optimal de $C$ et $L$, le taux auquel le travailleur est prêt à échanger/substituer des biens de consommation pour du loisir est égal au taux auquel le marché lui permet de le faire.

Nous pourrions également réécrire la condition précédente comme suit : $$\frac{MU_{L}}{w}=MU_{C}$$

Cette équation nous permet d’interpréter différemment la condition de tangence. Une heure de loisir supplémentaire augmente l’utilité du travailleur de $MU_{L}$, mais lui coûte $w$ euros (rappelons qu’il renonce à $w$ chaque fois qu’il alloue une heure au loisir plutôt qu’au travail). Ainsi, $\frac{MU_{L}}{w}$ mesure l’augmentation de l’utilité du travailleur lorsqu’il dépense un euro supplémentaire pour le loisir. En revanche, $MU_{C}$ mesure l’augmentation de son utilité lorsqu’il dépense un euro supplémentaire en biens de consommation. Ainsi, à l’offre optimale $(L^{\star},C^{\star})$, le prochain euro dépensé en loisirs doit valoir autant (en utilité) que le prochain euro dépensé en biens de consommation. Si ce n’est pas le cas, le travailleur pourrait faire mieux en choisissant un autre panier de loisirs et biens de consommation.

Que se passe-t-il lorsque le revenu non salarial change ?

Le revenu non salarial peut augmenter pour différentes raisons, telles que l’héritage, l’aide gouvernementale, les remises de fonds, etc. Cette augmentation élargit l’ensemble des opportunités du travailleur (l’ensemble des paniers qu’il peut s’offrir) et lui permet donc d’être mieux loti (d’atteindre un niveau d’utilité plus élevé).

La figure suivante illustre cette augmentation de l’utilité du travailleur.

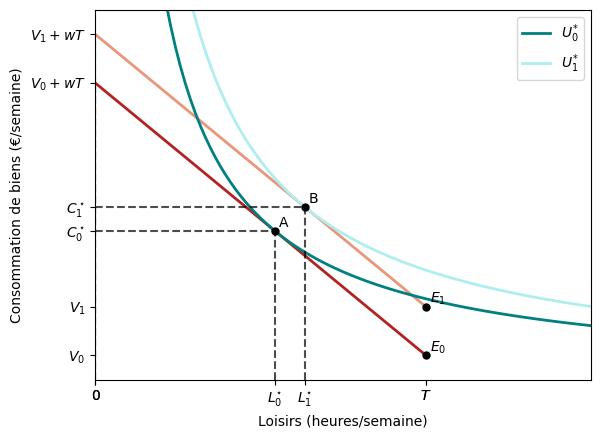
Il commence par la ligne budgétaire en rouge foncé et termine par celle en rouge clair. La première passe par le point de dotation $E_{0}$ tandis que la seconde passe par $E_{1}$. Néanmoins, les deux lignes budgétaires ont la même pente $-w$. En d’autres termes, nous permettons au revenu non salarial du travailleur d’augmenter de $V_{0}$ à $V_{1}$ tout en maintenant son salaire constant. Au nouveau panier optimal $B$, le travailleur utilise son revenu supplémentaire pour augmenter sa consommation de biens et de loisirs. Il choisit donc de travailler moins d’heures. L’effet d’une variation du revenu non salarial (à salaire constant) sur le nombre d’heures de loisir/travail est appelé effet de revenu. La figure ci-dessus montre le cas où le travailleur consomme plus de loisirs lorsque son revenu non salarial augmente, c’est-à-dire lorsque le loisir est un bien normal.

Un bien est normal lorsque l’augmentation du revenu, tous prix constants, entraîne une augmentation de sa consommation.

A partir de maintenant, nous ferons l’hypothèse que *le loisir est un bien normal. Par conséquent, les augmentations du revenu non salarial réduiront toujours le nombre d’heures de travail.

Que se passe-t-il lorsque le salaire change ?

Concentrons-nous maintenant sur l’effet d’une augmentation de salaire sur les heures de travail. Supposons que le salaire passe de $w_{0}$ à $w_{1}$, à revenu non salarial constant.

Comment cette augmentation modifie-t-elle la ligne budgétaire du travailleur ? Son revenu hors travail $V$ n’a pas changé. Il pourra donc toujours acheter des biens pour une valeur de $V$ même sans travailler, tout autant qu’auparavant. Néanmoins, s’il travaille, il pourra dépenser plus d’argent en biens pour chaque heure de travail. En d’autres termes, sa ligne budgétaire tourne autour de son point de dotation initial $E_{0}$. Cette rotation élargit également l’ensemble des opportunités du travailleur : il est désormais en mesure d’acheter un plus grand ensemble de paniers qu’auparavant.

Mais comment cet ensemble d’opportunités plus large modifie-t-il le choix optimal du travailleur en matière de loisirs (et donc d’heures de travail) ? Deux forces opposées entrent en jeu dans sa décision :

L’effet de revenu : Un salaire plus élevé augmente son revenu total, ce qui lui permet de consommer davantage de biens et de loisirs. Le loisir étant un bien normal, un revenu plus élevé augmente sa demande de loisirs, réduisant son temps de travail.
L’effet de substitution : Un salaire plus élevé augmente également le coût d’opportunité du loisir : chaque heure supplémentaire consacrée au loisir (plutôt qu’au travail) lui coûte plus cher ($w_{1}>w_{0}$). Par conséquent, un salaire plus élevé réduit sa demande de loisir, augmentant ses heures de travail.

Ainsi, une augmentation du salaire conduit à travailler davantage si l’effet de substitution domine l’effet de revenu. Ce cas est illustré dans la figure ci-dessous.

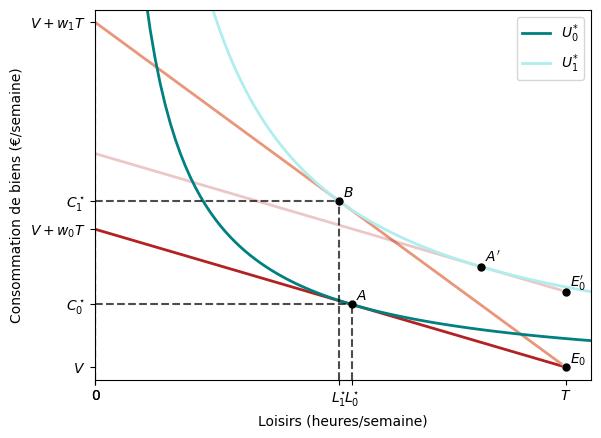
Lorsque le salaire du travailleur passe de $w_{0}$ à $w_{1}$, il choisit le panier $B$ au lieu de $A$. En outre, il choisit moins d’heures de loisir, $L_{1}^{\star}$ au lieu de $L_{0}^{\star}$ ; il travaille donc $L_{0}^{\star}-L_{1}^{\star}$ plus d’heures qu’auparavant.

Le passage du panier $A$ à $A^{\prime}$ montre l’effet de revenu, tandis que le passage de $A^{\prime}$ à $B$, l’effet de substitution.

Travailler ou ne pas travailler ?

Jusqu’à présent, nous avons supposé que l’individu avait choisi de travailler et qu’il choisissait son nombre optimal d’heures de travail. Mais pourrait-il préférer ne pas travailler du tout (être hors de la population active) ? Pour répondre à cette question, nous devons déterminer s’il est effectivement mieux en travaillant qu’en ne travaillant pas.

La figure suivante montre l’utilité de l’individu s’il ne travaille pas ($U_{0}$), c’est-à-dire s’il reste sur son point de dotation $E$, vivant de son revenu non salarial $V$.

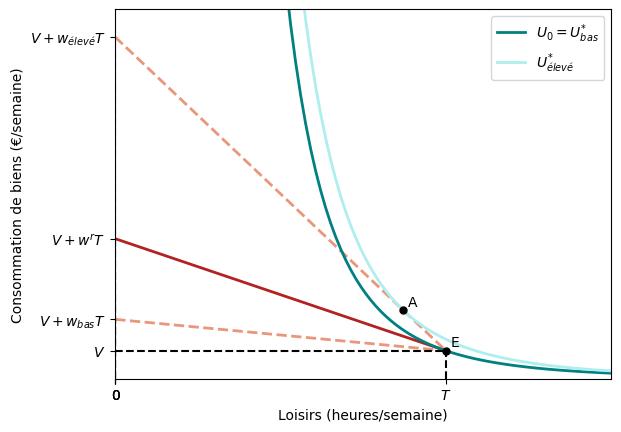
À $E$, son taux marginal de substitution des biens de consommation au loisir est de $-w^{r}$ : il a besoin de $w^{r}$ euros de biens pour renoncer à une heure de loisir (tout en gardant son utilité constante). Cette compensation monétaire $w^{r}$ est appelée salaire de réserve du travailleur.

Le salaire de réserve

Le salaire de réserve (noté $w^{r}$) est le salaire le plus bas auquel une personne est disposée à travailler. En d’autres termes, il s’agit du salaire qui laisse un individu indifférent à l’idée de travailler ou non.

$w^{r}$ répond donc à l’équation suivante : $$ U[C^{\star}(V,\boldsymbol{w^{r}}),L^{\star}(V,\boldsymbol{w^{r}})]=U[V,T]$$ où le côté gauche représente l’utilité pour l’individu de travailler et le côté droit, de ne pas travailler. La premiere découle du choix optimal de l’individu de travailler $T-L^{\star}$ heures, étant donné le revenu non salarial $V$ et le salaire $w^{r}$ ; tandis que la seconde découle de travailler zéro heures ($L^{\star}=T$).

$w^{r}$ est le salaire auquel ces niveaux d’utilité sont égaux.

Dans la figure ci-dessus, le salaire de réserve est égal à la pente de la courbe d’indifférence au point de dotation, en valeur absolue : $$w^{r}=|MRS_{C^{\star}=V,L^{\star}=T}|=-\left(-\frac{MU_{L}}{MU_{C}}\right)_{\bigr\rvert C^{\star}=V,L^{\star}=T}$$ Ainsi, $$w^{r}=\frac{MU_{L}}{MU_{C}}_{\bigr\rvert C^{\star}=V,L^{\star}=T}$$ C’est-à-dire qu’avec un salaire de $w^{r}$, le marché du travail rémunère l’individu juste assez pour qu’il accepte de renoncer à une heure de loisir et de travailler sa première heure. En conséquence, il choisit $C^{\star}=V$ et $L^{\star}=T$, ce qui signifie qu’il maximise son utilité en travaillant zéro heures. Cependant, pour tout salaire $w>w^{r}$, il choisirait de travailler un nombre positif d’heures.

Il est important de noter que cette dernière égalité peut ne pas tenir dans le cas de contraintes budgétaires plus complexes. Nous aborderons ces cas lorsque nous examinerons les effets des allocations de chômage sur les incitations au travail.

Les salaires inférieurs à $w^{r}$ découragent le travailleur de rejoindre le marché du travail puisque cela diminue son utilité. En revanche, un salaire plus élevé le convainc de travailler plutôt que de rester inactif en lui permettant d’atteindre une utilité plus élevée.

Ces deux cas sont représentés dans la figure ci-dessus. Les lignes en pointillé correspondent aux contraintes budgétaires auxquelles l’individu serait confronté avec un salaire relativement faible et élevé, $w_{bas}$ et $w_{élevé}$, respectivement. Avec $w_{bas}$, il a intérêt à ne pas travailler, il choisit donc de rester à son point de dotation $E$ et obtient l’utilité $U^{\star}_{bas}=U_{0}$. En revanche, sous $w_{élevé}$, il a intérêt à entrer sur le marché du travail et à choisir le panier $A$, ce qui lui donne une utilité $U^{\star}_{élevé}>U_{0}$.

En maintenant constant le salaire de réserve, des salaires plus élevés augmentent donc la probabilité de travailler.

Exercises

Les exercices suivants sont tirés du chapitre 2 du livre de George Borjas (voir syllabus).

Exercise 1

Simone tire de la satisfaction (ou “utilité”) de sa consommation de biens et services $(C)$ et de son temps de loisir $(L)$. Le nombre maximum d’heures de loisir qu’il peut consommer par semaine est de 110 heures. Sa fonction d’utilité est:

$$U(C,L) = C \times L.$$

Quel est son taux marginal de substitution du loisir pour la consommation ?

Et quel est son salaire de réserve s’il reçoit 660 € chaque semaine de la part de ses parents (quel que soit le nombre d’heures qu’il travaille)?

Exercise 2

Les préférences d’Anne pour la consommation (C) et les loisirs (L) peuvent être exprimées par la fonction d’utilité suivante :

$$U(C, L) = (C - 100) \times (L - 40)$$

Anne dispose de 110 heures par semaine à répartir entre le loisirs et le travail, avec un salaire après impôts de 10 €. Elle reçoit également 320 € d’allocations chaque semaine, indépendamment de ses heures de travail.

Questions à résoudre

Tracez la droite de budget d’Anne.
Quel est le taux marginal de substitution d’Anne lorsque L = 100 et qu’elle se trouve sur sa droite de budget ?
Quel est le salaire de réserve d’Anne ?
Déterminez les quantités optimales de consommation et de loisirs pour elle.

Last updated on 1 Sep, 2024