Application des politiques II

Subventions à la garde d’enfants

Ce chapitre s’appuie sur le chapitre 6 du livre de Blau et Winkler (voir syllabus).

Comme nous l’avons vu dans le dernier chapitre, la présence de jeunes enfants dans le ménage peut être un facteur dissuasif important pour la participation des femmes au marché du travail. Nous allons donc maintenant examiner l’effet des subventions à la garde d’enfants sur leur décision de travailler.

Le modèle de production domestique nous aide à prédire que ces subventions peuvent augmenter la probabilité que les femmes travaillent sur le marché.
Traçons cet effet. Nous montrerons d’abord comment les coûts de garde d’enfants peuvent réduire les incitations au travail, incitant certaines femmes à quitter la population active. Ensuite, nous montrerons comment la garde d’enfants subventionnée peut encourager certaines de ces femmes, qui autrement ne travailleraient pas, à commencer à travailler.

L’effet des coûts de garde d’enfants sur la participation au marché du travail

Supposons que Yannick, mère de jeunes enfants, gagne $w$ euros par heure si elle travaille sur le marché. Cependant, elle doit payer $c$ euros en services de garde pour chaque heure où elle n’est pas avec ses enfants.
Les coûts de garde d’enfants imposent donc une taxe sur son travail, réduisant son salaire net à $w-c$ euros/heure. En conséquence, ces coûts peuvent l’encourager à rester en dehors du marché du travail. Le graphique ci-dessous illustre cet effet négatif sur sa décision de travailler.

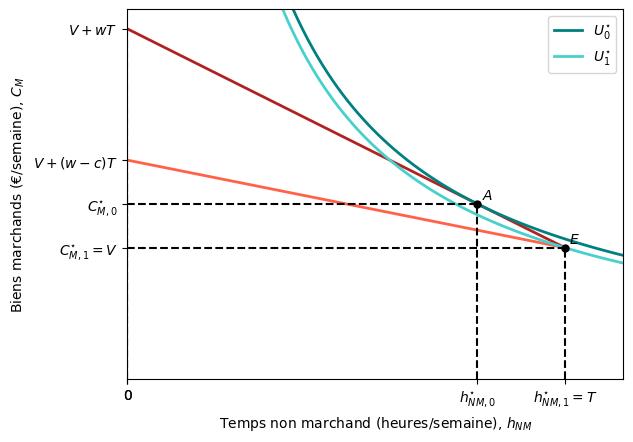
Avec un salaire net de $w$, Yannick maximise son utilité en choisissant le panier $A$, travaillant ainsi $T-h_{NM,0}^{\star}$ heures sur le marché du travail. Cependant, avec un salaire net de seulement $w-c$, elle maximise son utilité en restant à son point de dotation $E$, se retirant ainsi de la population active. Les coûts de garde d’enfants sont donc suffisamment élevés pour abaisser son salaire net en dessous de son salaire de réserve $(w-c<w^{r})$.

Deux forces entrent en jeu dans la décision de Yannick d’arrêter de travailler (passer de $A$ à $E$) : l’effet revenu et l’effet de substitution.
D’abord, les coûts de garde d’enfants diminuent son revenu : elle peut se permettre moins de paniers de $C_{M}$ et $h_{NM}$ lorsqu’elle gagne $w-c$ plutôt que $w$ par heure de travail. Par conséquent, elle diminue sa demande de temps non marchand (un bien normal) et augmente ses heures de travail (effet de revenu).
Ensuite, les coûts de garde d’enfants réduisent le prix du temps hors marché. Ce prix plus bas (coût d’opportunité plus failble) incite Yannick à augmenter sa demande de temps non marchand et à réduire ses heures de travail (effet de substitution).

Dans cet exemple, l’effet substitution est dominant et suffisamment fort pour pousser Yannick hors du marché du travail.

L’effet des subventions à la garde d’enfants sur la participation au marché du travail

Explorons maintenant comment Yannick pourrait réagir à la subvention des services de garde d’enfants. Le graphique ci-dessous montre son choix optimal lorsqu’elle reçoit une subvention de $s$ euros pour chaque heure de garde achetée sur le marché.

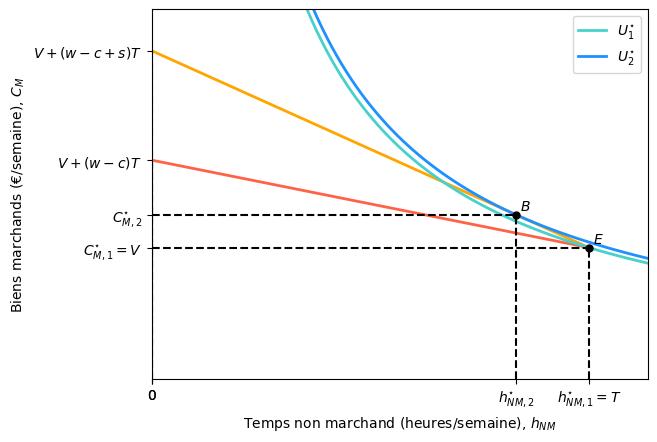
Sans subvention, Yannick reçoit un salaire net de $w-c$ euros/heure. À ce salaire, elle maximise son utilité en restant à son point de dotation $E$, donc hors du marché du travail. C’est le choix optimal dont nous avons parlé auparavant. Cependant, avec la subvention, elle reçoit un salaire net de $w-c+s$. Avec ce salaire plus élevé, elle maximise son utilité en se déplaçant au panier $B$, rejoignant ainsi la population active et travaillant $T-h_{NM,2}^{\star}$ heures. La subvention est donc suffisamment élevée pour augmenter son salaire net au-dessus de son salaire de réserve $(w-c+s>w^{r})$.

Pourquoi Yannick choisit-elle de passer de $E$ à $B$ ?
La subvention à la garde d’enfants augmente le coût d’opportunité de son temps non marchand, l’encourageant ainsi à réduire les heures qu’elle consacre aux activités hors marché et à commencer à travailler.

Quel est l’effet des subventions à la garde d’enfants sur les heures de travail des mères qui sont déjà dans la population active ?

Pour les mères inactives, les subventions à la garde d’enfants augmentent sans ambiguïté la probabilité qu’elles entrent sur le marché du travail, par un effet de substitution. En revanche, pour les mères actives, ces subventions ont un effet ambigu sur leurs heures de travail. En particulier, ces mères ne travailleront plus d’heures que si l’effet de substitution domine l’effet revenu.

Pourquoi pouvons-nous faire une prédiction claire concernant l’effet des subventions à la garde d’enfants sur la participation au marché du travail, mais pas sur les heures travaillées ? Parce qu’une augmentation des salaires nets (ici, en raison d’une garde d’enfants subventionnée) ne crée un effet revenu que si l’individu travaille déjà sur le marché. Si ce n’est pas le cas, une augmentation de son salaire net n’a aucun effet sur son revenu réel.

Exercises

Exercise 1

Cet exercice est tiré du chapitre 7 du livre de Tito Boeri et Jan Van Ours (voir syllabus).

Les préférences d’Elena pour les biens achetés sur le marché $(C)$ et les biens produits à la maison $(D)$ peuvent être exprimées comme suit : $$U = CD$$

Elena dispose de 100 heures par semaine à répartir entre le travail sur le marché et la production domestique. Elle peut produire des biens domestiques $D$ à l’aide de la technologie suivante : $$f(h_{D}) =\sqrt h_{D}$$

où $h_{D}$ désigne les heures qu’elle consacre au travail domestique.

1. Quelle est sa répartition optimale du temps entre le travail sur le marché et la production domestique si elle gagne 10 euros de l’heure ?
2. Supposons maintenant qu’Elena ait un enfant. Etant donné la valeur supplémentaire du temps passé avec son enfant, sa fonction d’utilité devient $U = CD^2$.
   Par ailleurs, toute heure passée loin de son enfant implique un coût de 5 euros à payer à une baby-sitter.
   Comment cela affecte-t-il la répartition de son temps entre le travail et la maison ?