Application des politiques I

L’allocation chômage

L’allocation chômage vise à protéger les travailleurs contre la perte de revenus. Néanmoins, ce soutien au revenu peut les décourager de reprendre le travail. Pour faire face à ces potentiels effets dissuasifs sur le travail, l’allocation chômage est généralement accordée sous les conditions suivantes.

Critères d’admissibilité : Pour y être éligible, vous devez avoir été licencié par votre employeur et avoir travaillé pendant une durée minimale.
Générosité :
- Niveau : L’allocation chômage remplace généralement un pourcentage fixe de vos revenus précédents, bien que ce pourcentage puisse diminuer progressivement au fil du temps.
- Durée : L’allocation est souvent limitée dans le temps. Elle est versée pour des périodes plus longues à ceux qui ont travaillé plus longtemps dans le passé (qui ont de plus longues périodes de cotisations) et à ceux qui sont plus âgés.
Conditionnalité : Les bénéficiaires sont souvent tenus de remplir un ensemble de conditions pour conserver leur droit à l’allocation.

Par exemple, vous pouvez être tenu de justifier tout refus d’emploi et de participer à des programmes de formation et à des entretiens de conseil. De plus, vous pouvez également devoir prouver que vous recherchez activement un emploi.

Nous allons maintenant explorer pourquoi l’allocation chômage peut réduire les incitations au travail et comment les conditions mentionnées ci-dessus pourraient être justifiées. Nous commencerons par utiliser le modèle néoclassique travail-loisir que nous avons vu dans le chapitre précédent. Ensuite, nous utiliserons la théorie de la recherche d’emploi.

Pourquoi encore une autre théorie pour comprendre comment l’allocation chômage modifie les incitations au travail ?

Le modèle néoclassique travail-loisir suppose implicitement qu’un individu peut trouver un emploi immédiatement s’il choisit d’entrer sur le marché du travail. Dans ce modèle, l’individu doit simplement choisir entre entrer dans la population active ou rester en dehors. Choisir d’entrer signifie être employé, tandis que rester en dehors signifie ne pas avoir d’emploi ni en chercher un (malgré la capacité de travailler).

Le modèle exclut donc l’existence du chômage. Par conséquent, discuter de l’allocation chômage dans ce cadre néoclassique pourrait sembler incohérent. Pourtant, malgré cette limitation, ce cadre peut nous donner une première idée des effets de cette allocation sur les incitations des gens à travailler.

Plus tard, nous introduirons la théorie de la recherche d’emploi, qui repose sur l’hypothèse plus réaliste que la recherche d’un emploi prend du temps et des efforts.

L’allocation chômage et la décision de travailler : Le modèle néoclassique travail-loisir

Comme dans le chapitre précédent, nous supposons toujours ce qui suit :

L’individu (travailleur) aime consommer des biens $(C)$ et des loisirs $(L)$, comme le capture la fonction d’utilité : $$U(C,L)$$
Il a des ressources limitées (temps et revenu) : $$T = L + h$$ $$C = V + wh$$ ce qui donne la contrainte budgétaire suivante : $$C = (V + wT) - wL$$ où :

$T$ : temps total disponible (pendant une période donnée),

$h$ : heures de travail,

$V$ : revenu non salarial,

$w$ : le salaire.
Il choisit $C$ et $L$ de manière à maximiser son utilité étant donné sa contrainte budgétaire.

Imaginons maintenant que le gouvernement introduise une allocation chômage $b$. Par conception, cette allocation est conditionnée au fait de ne pas travailler. Le revenu non salarial serait alors égal à $V+b$.

Les figures suivantes illustrent l’effet de cette allocation sur les incitations de l’individu à rejoindre la population active.

Sans allocation:

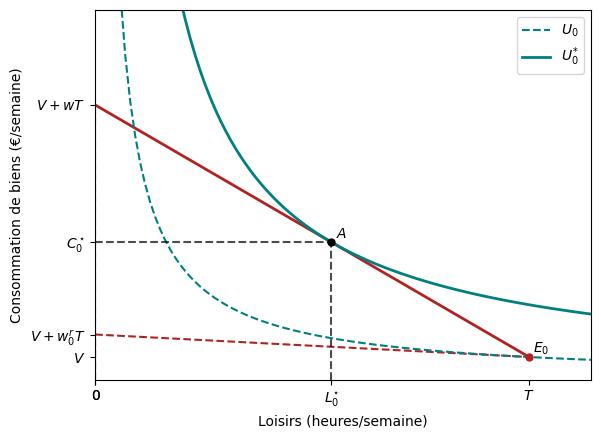
Avec allocation:

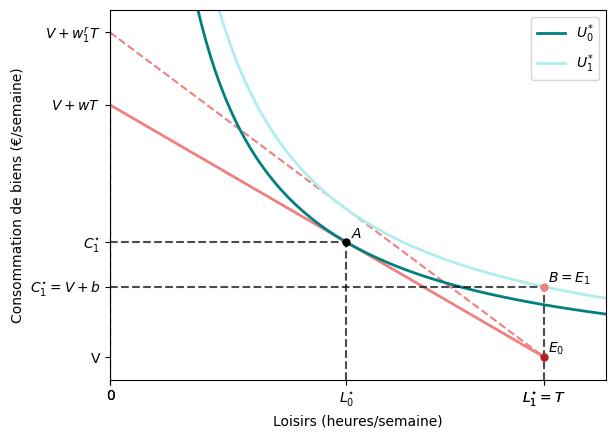
Elles montrent son choix optimal sans et avec l’allocation.

L’allocation chômage $b$ modifie la contrainte budgétaire de l’individu en déplaçant son point de dotation de $E_{0}$ à $E_{1}$. Néanmoins, une fois qu’il entre sur le marché du travail, sa contrainte budgétaire revient à celle d’origine.

Ce type d’allocations peut conduire certaines personnes à quitter la population active. Comme illustré dans la figure, l’individu est en effet mieux loti en ne travaillant pas et en réclamant des allocations qu’en travaillant pour un salaire $w$ (comme il le faisait auparavant).

L’allocation chômage augmente le salaire de réserve de l’individu en améliorant son point de dotation. Son nouveau salaire de réserve $w^{r}_{1}$ est plus élevé que celui qu’il avait initialement, $w^{r}_{0}$, lorsqu’aucune allocation ne lui était offerte.

Cette augmentation du salaire de réserve réduit donc la probabilité que les travailleurs à bas salaires choisissent de reprendre le travail. Il est important de noter que nous pouvons faire cette prédiction sans aucune hypothèse sur les préférences des travailleurs à bas salaires. Nous ne disons pas vraiment qu’ils arrêteront de travailler parce que le loisir a beaucoup plus de valeur pour eux. Nous disons simplement que, étant donné leur rendement du travail plus faible (salaire plus bas), ils peuvent se trouver mieux lotis en s’appuyant sur l’allocation chômage plutôt qu’en restant sur le marché du travail.

Pour fixer les idées, il peut être utile de refaire notre analyse précédente mais avec un changement mineur. Supposons que l’allocation de chômage offerte à l’individu est égale à son revenu du travail précédent. Ce niveau de prestation lui permet essentiellement de consommer autant qu’avant mais sans avoir besoin de travailler, ce qui augmente forcément son niveau d’utilité.

La figure ci-dessous illustre ce cas.

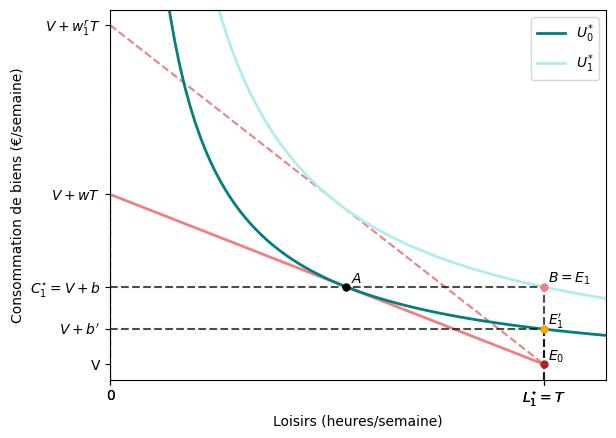
L’individu atteint une utilité plus élevée sur son nouveau point de dotation $E_{1}$ car il peut dépenser autant d’argent qu’avant pour des biens, tout en profitant de plus de loisirs (en fait, de tout le loisir qu’il peut avoir !). Cette allocation généreuse augmente son salaire de réserve au-dessus de son salaire de marché antérieur $(w^{r}_{1}>w).$ Rappelez-vous que le salaire de réserve est le salaire qui laisse l’individu indifférent entre travailler et ne pas travailler.

Étant donné les préférences de l’individu illustrées dans la figure, une allocation juste en dessous de $b^{\prime}$ le protégerait contre la perte de revenus tout en l’encourageant à reprende le travail. En effet, une telle prestation l’assurerait presque entièrement contre la perte de revenu en lui permettant d’atteindre quasiment le même niveau d’utilité qu’auparavant. Cependant, cette allocation maintiendrait toujours son incitation à reprendre le travail : travailler lui permettrait d’atteindre son utilité initiale $U^{*}_{0}$, alors que ne pas travailler et recevoir une allocation juste en dessous de $b^{\prime}$ ne le permettrait pas.

En pratique, cependant, déterminer la valeur de $b^{\prime}$ est un défi. Les travailleurs ont des préférences différentes, ce qui signifie que l’allocation optimale pour maintenir les incitations au travail varie. Les décideurs politiques doivent donc se contenter de fixer l’allocation chômage comme une fraction des revenus précédents et de la lier à des exigences de recherche d’emploi et autres, qui sont souvent difficiles à mettre en œuvre.

Autres programmes sociaux : Allocations sociales permettant de travailler

Les allocations de chômage sont un type d’allocations sociales offertes à condition de ne pas être employé. Ces allocations sans travail peuvent être reçues en raison d’un licenciement (comme dans le cas de l’allocation chômage), d’une blessure temporaire au travail ou d’une invalidité permanente. Elles peuvent également être reçues en cas de pauvreté, telle que définie par un seuil de revenu minimum fixé par le gouvernement.

Quelle que soit la raison pour avoir droit à ces allocations, elles augmentent toutes le salaire de réserve de leurs bénéficiaires et diminuent donc la probabilité qu’ils (ré)intègrent le marché du travail (en particulier s’ils occupent des emplois à bas salaires). Mais que se passerait-il si les personnes pouvaient encore se qualifier pour ces prestations, au moins partiellement, même si elles reprenaient le travail ?

Bien que cette allocation ne serait plus qualifié d’allocation chômage, il est toujours instructif d’examiner comment elle pourrait affecter les incitations au travail. Considérons deux cas :

a) Le travailleur perd 50 centimes des allocations $b$ pour chaque euro gagné sur le marché du travail, et

b) Le travailleur perd un euro des allocations $b$ pour chaque euro gagné, mais seulement tant que son revenu est inférieur à un certain seuil.

Cas A :

La figure suivante illustre le premier cas.

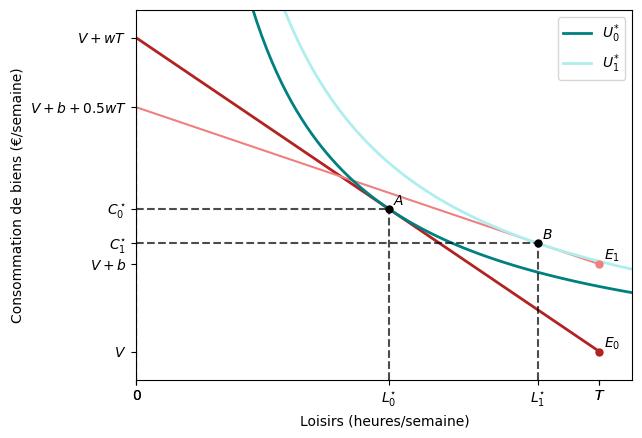
La figure montre le choix optimal du travailleur sans et avec allocations (paniers $A$ et $B$, respectivement). Étant donné les préférences du travailleur illustrées dans la figure, il est mieux loti avec $B$ qu’avec $A$. En d’autres termes, il préférera continuer à bénéficier des allocations et à travailler moins d’heures qu’auparavant. Par conséquent, ces allocations sociales peuvent également créer des désincitations au travail en encourageant les gens à travailler moins d’heures qu’ils ne l’auraient fait en l’absence d’allocations.

Pourquoi ? Ces allocations modifient la contrainte budgétaire de deux façons. Premièrement, elles déplacent le point de dotation de $E_{0}$ à $E_{1}$, créant un effet de revenu qui augmente la demande de loisirs du travailleur et diminue ses heures de travail. Deuxièmement, elles diminuent la pente de la contrainte budgétaire. En effet, le fait que le travailleur perde 50 centimes des allocations pour chaque euro gagné implique que son nouveau salaire net est de 50% de celui qu’il avait initialement ($w$ dans la figure). Cette “taxe” de 50 pour cent sur le revenu du travail réduit le coût d’opportunité du loisir, créant ainsi un effet de substitution : le travailleur choisit de consommer plus de loisirs et donc de travailler moins.

Cet exemple simple suggère que les prestations sociales peuvent non seulement réduire la probabilité que les bénéficiaires travaillent mais aussi le nombre d’heures de travail de ceux qui choisissent de rejoindre la population active.

Cas B :

Considérons maintenant le deuxième cas, où le travailleur perd un euro des allocations pour chaque euro gagné en travaillant. Ce cas, illustré ci-dessous, est celui d’un programme d’aide sociale visant à garantir un revenu minimum (égal à $V+b$ dans la figure). Si la personne éligible ne travaille pas, elle reçoit $b$, ayant ainsi un revenu total de $V+b$. Sinon, le gouvernement lui verse le montant nécessaire pour atteindre le revenu minimum. Une fois ce seuil atteint, la personne n’est plus éligible à cette aide sociale.

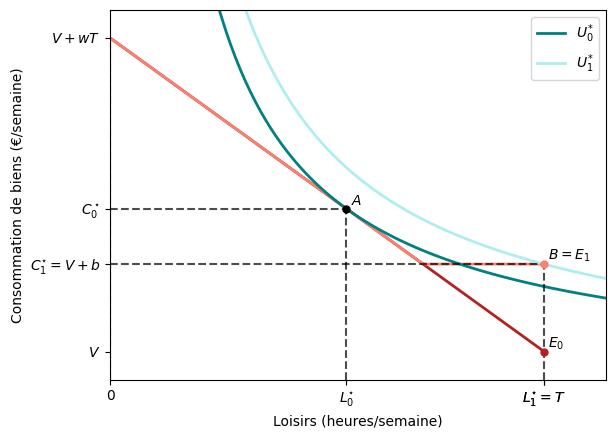
Comme précédemment, la figure montre le choix optimal du travailleur sans et avec allocations (ensembles $A$ et $B$, respectivement). Comme illustré dans la figure, le travailleur est mieux loti avec le panier $B$ qu’avec $A$. C’est-à-dire qu’il est plus heureux de réclamer des allocations et de rester inactif que d’abandonner l’aide sociale et de travailler autant qu’il le faisait ou qu’il l’aurait fait en l’absence de cette aide.

Ce résultat ne devrait pas être surprenant étant donné celui que nous avons discuté précédemment. En effet, nous représentons les préférences du même travailleur, avec la même contrainte budgétaire initiale et le même niveau d’allocation $b$. Comme auparavant, cette allocation crée un effet de revenu réduisant les heures de travail. Néanmoins, le gouvernement prend maintenant un euro au lieu de 50 centimes des allocations du travailleur pour chaque euro qu’il gagne (et tant qu’il est éligible à l’aide sociale). C’est-à-dire que le gouvernement impose maintenant le salaire du travailleur à un taux de 100 au lieu de 50 pour cent ! Cette taxe de 100 pour cent induit un énorme effet de substitution : le coût d’opportunité du loisir tombe à zéro, décourageant ainsi les bénéficiaires de l’aide sociale de travailler !

Avant de clore ce chapitre, il vaut la peine de noter que les désincitations au travail que nous avons discutées précédemment peuvent ne pas se produire avec des salaires de marché plus élevés ou des préférences plus faibles pour le loisir. Les figures suivantes illustrent le rôle de ces dernières dans le cadre des allocations visant à garantir un revenu minimum.

Préférence plus élevée pour le loisir:

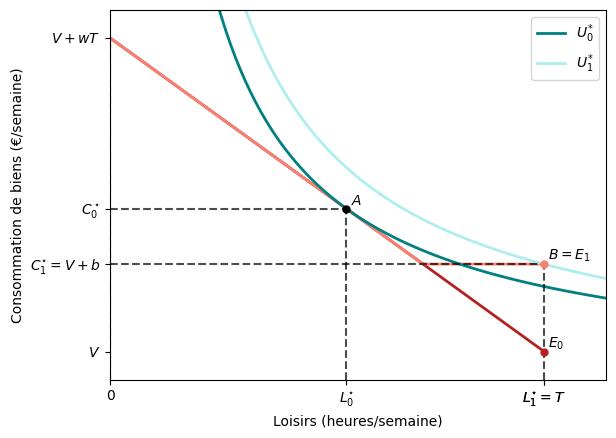
Préférence plus faible pour le loisir:

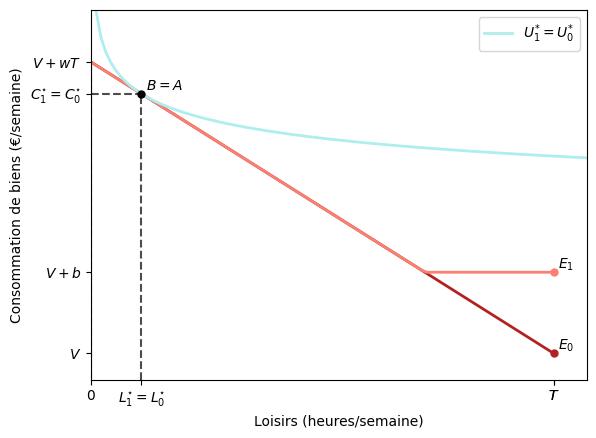
Elles montrent le choix optimal de loisir pour un travailleur ayant une préférence relativement élevée et faible pour le loisir. Ces travailleurs ne diffèrent que par leurs préférences et non par les contraintes budgétaires auxquelles ils font face avec et sans allocations. Comme le montre la figure, les travailleurs ayant une faible préférence pour le loisir peuvent ne pas changer du tout leur décision de travailler, même si on leur offre des allocations $b$. En effet, le travailleur représenté sur la deuxième figure maximise son utilité en travaillant $T-L^{*}_{1}$ heures, au lieu de demander l’aide sociale.

L’allocation chômage et la décision de chercher du travail : Un modèle de recherche d’emploi

Le modèle néoclassique travail-loisir que nous avons vu précédemment suppose que les individus peuvent trouver un emploi immédiatement s’ils choisissent de travailler. Ce modèle nous aide donc à comprendre les effets des allocations sociales sur la décision des individus de rejoindre la population active, mais pas sur leur décision de continuer à chercher du travail, et donc de rester au chômage.

Rappel

Un chômeur est défini comme quelqu’un qui n’est pas employé mais qui souhaite travailler et recherche activement un emploi.

Dans le modèle travail-loisir, les chômeurs n’existent pas vraiment puisque, par hypothèse, on peut trouver un emploi immédiatement. Dans ce modèle, les personnes sont soit employées soit hors de la population active.

Dans cette section, nous présentons le modèle de base de la recherche d’emploi qui repose sur l’hypothèse plus réaliste que les individus doivent investir du temps et des efforts pour trouver un emploi. Ce modèle permet de comprendre comment les allocations de chômage peuvent modifier les décisions de recherche d’emploi des individus et, en fin de compte, leur durée de chômage. En particulier, nous examinerons comment les allocations de chômage peuvent affecter le degré d’exigence des personnes dans le choix de leur emploi et l’intensité de leur recherche d’emploi.

L’hypothèse sous-jacente du modèle de recherche d’emploi est que les personnes disposent d’informations imparfaites sur quelles entreprises offrent des emplois qui leur conviennent, de sorte qu’elles passent du temps à chercher qui offre quoi. Dans ce modèle, différentes entreprises offrent des salaires différents au même travailleur. Les personnes souhaitant travailler sont donc encouragées à rechercher des emplois mieux rémunérés jusqu’à ce qu’elles trouvent une offre salariale “suffisante”. Ce processus de recherche d’emploi ressemble à la recherche d’un appartement à louer : on ne sait pas vraiment qui offre quoi, alors on cherche autour de soi, en essayant de trouver le meilleur loyer possible, mais on arrête de chercher une fois qu’on a trouvé une offre “suffisamment bonne”.

Dans le modèle de recherche d’emploi, les chercheurs d’emploi font deux choix différents. Premièrement, ils choisissent à quel point ils sont “exigeants” dans leur recherche d’emploi : quel est le salaire minimum qu’ils sont prêts à accepter pour cesser de chercher de nouvelles offres d’emploi ? Deuxièmement, ils choisissent l’intensité de leur recherche d’emploi : combien d’heures par jour doivent-ils consacrer à contacter des agences pour l’emploi, à envoyer des candidatures, à se rendre à des entretiens d’embauche, etc.

Ces deux choix, à leur tour, influencent la probabilité de quitter le chômage et de commencer à travailler. Pour comprendre pourquoi, notons que cette probabilité (notée $\phi$) dépend de :

la probabilité de recevoir une offre d’emploi $(\lambda)$ et
la probabilité de l’accepter $(\gamma).$

Plus précisément,

$$\phi = \lambda \gamma$$

Dans le modèle de recherche d’emploi, les choix des personnes influencent cette probabilité de deux manières :

ils peuvent chercher davantage et augmenter ainsi leurs chances de recevoir une offre d’emploi $(\lambda)$ ou
ils peuvent devenir moins “exigeants” quant aux offres qu’ils acceptent et donc augmenter leurs chances d’accepter un emploi $(\gamma).$

Bien que les demandeurs d’emploi puissent choisir à la fois l’intensité de leur recherche et leur degré d’exigence, pour simplifier, nous n’examinerons qu’un seul choix à la fois.

La discussion qui suit s’inspire largement du chapitre 12 du livre de George Borjas et du chapitre 7 de celui de Bruno Van der Linden (voir le syllabus).

Choisir à quel point être “exigeant” : le salaire demandé

Concentrons-nous sur un seul individu ayant un ensemble donné de compétences et souhaitant travailler. Comme nous l’avons dit précédemment, nous supposons que cette personne peut travailler pour différentes entreprises, payant différents salaires, mais qu’elle ne sait pas qui paie quoi. Néanmoins, nous supposons que l’individu connaît la distribution des offres salariales qui lui sont proposées sur le marché du travail. En d’autres termes, elle connaît le salaire minimum et le salaire maximum qu’elle peut obtenir compte tenu de ses compétences, ainsi que la probabilité cumulée de tout salaire situé entre les deux. La figure ci-dessous représente une distribution typique d’offres salariales, dans laquelle nous avons supposé un salaire minimum et maximum de 5 et 25 euros, respectivement.

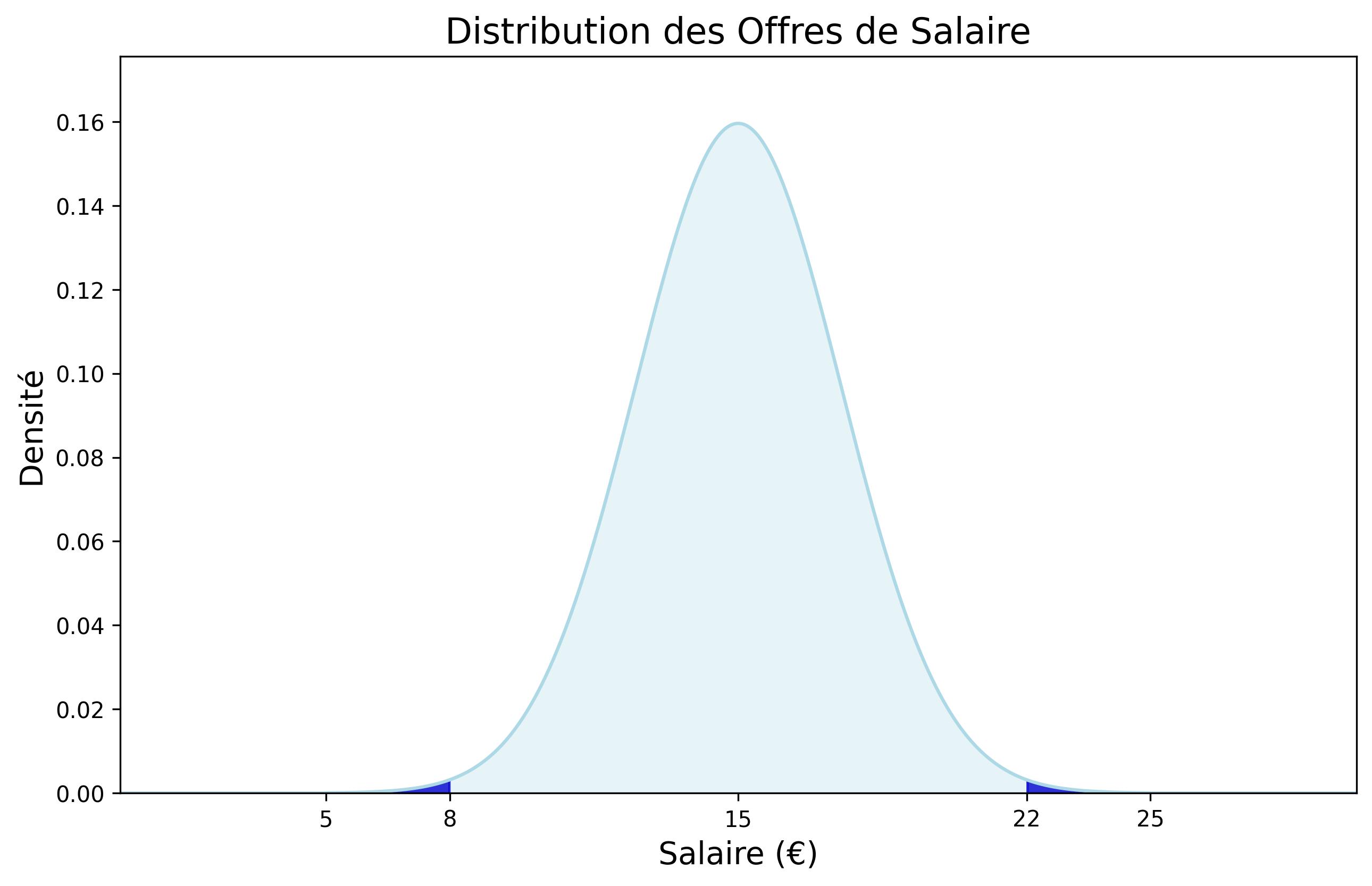
Comme l’individu connaît la forme de cette distribution, il sait qu’il a peu de chances de trouver un emploi payé moins de 8 euros ou plus de 22 euros (la probabilité de trouver ces offres est représentée par la zone en bleu foncé dans la figure ci-dessus). La forme de cette distribution reflète simplement le fait que les options “extrêmement mauvaises” ou “extrêmement bonnes” sont rares.

Bien que l’individu puisse être tenté de continuer à chercher jusqu’à ce qu’il trouve la “bonne grosse” affaire (ici, l’emploi payé 25 euros), il reconnaît que la recherche est coûteuse. Les coûts de recherche comprennent les coûts directs, tels que les billets de transport pour les entretiens d’embauche, mais aussi le coût d’opportunité de continuer à chercher au lieu de travailler pour un salaire. En effet, chaque fois que l’individu choisit de rejeter une offre de salaire donnée, disons de $w$ euros, il renonce à $w$ euros de revenu. Plus le salaire proposé est élevé, plus élevé est son coût d’opportunité de continuer à chercher de meilleures offres. L’individu est donc confronté à un compromis : plus il cherche longtemps, plus il a de chances de trouver une offre salariale élevée, mais plus sa recherche est coûteuse.

À quel moment doit-il se contenter de l’offre salariale sous la main et cesser de chercher un emploi ? Il doit le faire lorsqu’il trouve une offre salariale supérieure au seuil minimum, appelé “salaire demandé”. Pour comprendre comment l’individu fixe ce salaire demandé, nous devons réfléchir aux coûts et aux avantages de la poursuite de la recherche d’un emploi. Comme nous le verrons, le salaire demandé est le salaire auquel le bénéfice marginal est égal au coût marginal de la recherche (disons de chercher encore une semaine). Pour tout salaire supérieure au salaire demandé, les coûts de poursuivre la recherche l’emportent sur les bénéfices.

Le coût marginal de la recherche

Comme nous l’avons noté précédemment, plus élevée l’offre salariale à la main, plus élevé le coût d’opportunité d’une recherche supplémentaire. Par conséquent, le coût marginal de la recherche $(MC)$ est une fonction croissante du salaire disponible, comme le montre la figure ci-dessous.

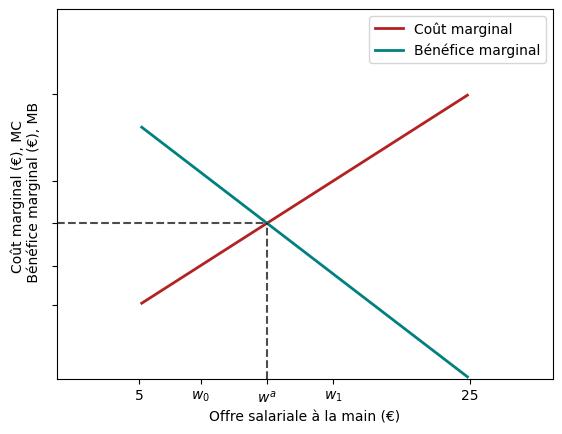
Le bénéfice marginal de la recherche

En revanche, plus élevée l’offre salariale à la main, plus faible le gain attendu d’une recherche supplémentaire. En effet, meilleure est l’offre que nous trouvons, moins nous avons de chances de faire encore mieux. Supposons que l’individu trouve l’emploi le mieux rémunéré, soit 25 euros dans la figure ci-dessus. Le gain marginal de continuer à chercher est nul puisqu’il n’y a aucune chance qu’elle trouve un salaire plus élevé. À l’autre extrême, disons que la personne n’a pas de chance et trouve l’emploi le moins bien payé, soit 5 euros. Dans ce cas, le gain marginal de continuer à chercher est substantiel puisque les chances de trouver un emploi rémunéré à plus de 5 euros sont assez élevées.

Le bénéfice marginal de la recherche $(MB)$ est donc une fonction décroissante du salaire disponible, comme le montre la figure ci-dessus.

Le salaire demandé

Comme la figure le révèle, le salaire demandé $(w^{a})$ rend l’individu indifférent entre accepter une offre et poursuivre sa recherche d’emploi.
Pour comprendre pourquoi, supposons que l’individu reçoive une offre d’emploi payée $w_{0}<w^{a}$. Devrait-elle se contenter de ce salaire et cesser de chercher des salaires plus élevés ? Non, car le bénéfice marginal de la recherche est supérieur au coût marginal. Elle doit donc continuer à chercher de meilleurs emplois. Imaginons maintenant que l’individu reçoive une offre salariale de $w_{1}>w^{a}$. Dans ce cas, elle devrait accepter l’offre et cesser de chercher parce que le bénéfice marginal de la recherche est inférieur au coût marginal.

Comment les allocations de chômage changent-elles le salaire demandé ?

Comme nous l’avons vu auparavant, le fait de chercher plus longtemps de meilleurs emplois entraîne à la fois des coûts directs et un coût d’opportunité. Au lieu de poursuivre sa recherche, un demandeur d’emploi pourrait accepter l’offre de salaire qui lui est faite. Ainsi, le coût d’opportunité d’une recherche prolongée est le revenu auquel le demandeur d’emploi renonce en n’acceptant pas son offre actuelle. Mais si elle reçoit $b$ euros par mois pendant qu’elle cherche un emploi en tant que chômeuse, elle renonce à un revenu de juste $\phantom{|}w-b$ euros par mois. En d’autres termes, elle renonce à son offre salariale actuelle net des allocations chômage.

Les allocations de chômage réduisent donc le coût marginal de la recherche d’emploi, ce qui augmente le salaire demandé. Ce salaire demandé plus élevé entraîne à son tour des périodes de chômage plus longues. Étant donné que les gens n’acceptent que des emplois dont le salaire est supérieur à leur salaire demandé, plus élevé ce salaire, plus faible est la probabilité qu’ils acceptent les offres d’emploi qui leur sont faites.

Les décideurs politiques sont donc confrontés à un compromis : des allocations de chômage plus élevées offrent une meilleure assurance contre la perte d’emploi mais diminuent les incitations à accepter les offres d’emploi entrantes, prolongeant ainsi le chômage.

Choisir l’intensité de la recherche d’emploi : Effort de recherche

Dans notre discussion précédente sur le salaire demandé, nous avons ignoré l’effort de recherche d’emploi. Nous avons implicitement supposé que l’individu n’avait aucun contrôle sur le nombre d’offres salariales qu’elle recevait, mais seulement sur celles qu’elle était prête à accepter.

Nous supposons donc à présent que si elle cherche davantage (par exemple, en consacrant plus d’heures par semaine à la recherche d’un emploi), elle reçoit plus d’offres salariales ou, alternativement, qu’elle a une probabilité plus élevée d’en recevoir une. Néanmoins, nous supposons également qu’il est coûteux de chercher davantage.

Soit $e$ le niveau d’effort de recherche d’emploi.

Le coût marginal de l’effort de recherche

Nous supposons que l’effort de recherche est de plus en plus coûteux.
Laissons $C(e)$ désigner le coût de l’effort, y compris les coûts monétaires et non monétaires (par exemple, les billets de transport pour les entretiens d’embauche, les coûts psychologiques et le temps de loisir perdu).
Nous supposons donc que le coût marginal de l’effort, $C^{\prime}(e)$, est positif et croissant.

Le bénéfice marginal de l’effort de recherche

Nous supposons qu’une recherche plus intensive est payante, mais à un taux décroissant. Un effort accru est bénéfique pour le demandeur d’emploi parce que :

il augmente ses chances de recevoir des offres d’emploi, et
les offres d’emploi sont avantageuses.

Plus précisément, nous faisons les hypothèses suivantes :

Une unité d’effort supplémentaire augmente la probabilité de recevoir une offre mais moins que la précédente.
Soit $\lambda(e)$ la probabilité de recevoir une offre d’emploi avec un niveau d’effort $e.$
Nous supposons donc que $\lambda^{\prime}(e)$ est positif mais décroissante.
Si l’individu ne reçoit pas d’offre d’emploi, il demande des allocations de chômage $b$ et cesse de chercher (il n’y a pas de sanctions pour ceux qui ne cherchent plus d’emploi). Cependant, si elle reçoit une offre $w$, elle l’accepte car nous supposons que cette offre est meilleure que la demande d’allocations. En particulier,

$$v(w)-v(b)>0$$

où :
- $v(w)$ : l’utilité d’obtenir une offre rémunérée au salaire $w$
- $v(b)$ : l’utilité de recevoir des allocations de chômage $b$.

Par conséquent, l’espérance de bénéfice de choisir l’effort $e$ est :

$$\lambda(e)v(w) + (1-\lambda(e))v(b)$$

et le bénéfice marginal de l’effort :

$$\lambda^{\prime}(e)[v(w)-v(b)] >0$$

En d’autres termes : les bénéfices d’une unité supplémentaire d’effort sont les chances additionnelles d’obtenir un emploi qui en découlent fois la valeur de cet emploi par rapport aux allocations chômage.

Le niveau optimal d’effort

L’individu choisit le niveau d’effort qui maximise l’espérance de son utilité nette de coûts :

$$\lambda(e)v(w) + (1-\lambda(e))v(b) - C(e)$$

Par conséquent, l’effort optimal $(e^{*})$ vérifie la condition du premier ordre suivante :

$$\lambda^{\prime}(e^{\star})v(w) - \lambda^{\prime}(e^{\star})v(b) - C^{\prime}(e^{\star}) = 0$$

$$\lambda^{\prime}(e^{\star})[v(w)-v(b)] = C^{\prime}(e^{\star}) $$

Comment les allocations chômage changent-elles l’effort optimal ?

La condition précédente montre que l’individu cherchera davantage lorsqu’il est confronté à un coût marginal de l’effort plus faible. En outre, il cherchera également plus intensément lorsqu’il percevra un salaire plus élevé net des allocations. Par conséquent, des allocations de chômage plus généreuses réduisent l’effort de recherche d’emploi. Cet effort de recherche plus faible diminue la probabilité de recevoir des offres d’emploi, prolongeant ainsi le chômage.

Exercises

Le modèle néoclassique travail-loisir

L’exercice suivant est tiré du Chapitre 12 du livre de Tito Boeri et Jan van Ours (voir syllabus).

Exercise 1

La fonction d’utilité de Juan pour la consommation $C$ et le loisir $L$ est :

$$U(C,L) = C \times L.$$

Il dispose de 168 heures dans la semaine, n’a pas de revenu non salarial mais peut gagner 15 euros par heure s’il choisit de travailler.

Ecrivez la contrainte budgétaire de Juan et représentez-la sur un graphique.
Quelle est son niveau optimal de consommation et de loisir ?
Supposons maintenant que Juan perde son emploi et ait droit à 320 euros d’allocations chômage par semaine.
Qu’adviendra-t-il de sa décision de travailler s’il reçoit à nouveau une offre d’emploi de 15 euros par heure ?
En particulier, choisira-t-il de retourner au travail ou préférera-t-il rester sans emploi et demander des allocations de chômage ?
Quelle est la valeur des allocations de chômage qui rendrait Juan indifférent à l’idée de reprendre le travail ou non ?

Le modèle de recherche d’emploi

L’exercice suivant est tiré du Chapitre 12 du livre de George Borjas (voir syllabus).

Exercise 2

Supposons que le bénéfice marginal de la recherche soit

$$MB = 50 - 1.5w,$$

où $w$ est l’offre salariale disponible. Le coût marginal de la recherche est de

$$MC = 5 + w.$$

Pourquoi le bénéfice marginal de la recherche est-il une fonction négative de l’offre salariale disponible ?
Pouvez-vous donner une interprétation économique de l’ordonnée à l’origine dans l’équation du coût marginal ; en d’autres termes, que signifie le fait que l’ordonnée à l’origine est égale à 5 euros ?
De même, que signifie le fait que la pente dans l’équation du coût marginal est égale à 1 euro ?
Quel est le salaire demandé par l’individu’? Acceptera-t-il une offre d’emploi de 15 euros ?
Supposons que les allocations chômage soient réduites, ce qui entraîne une augmentation du coût marginal de la recherche à $MC = 20 + w.$ Quel est le nouveau salaire demandé ? L’individu acceptera-t-il une offre d’emploi de 15 euros ?

Last updated on 1 Sep, 2024